近日，公共卫生学院王伟教授团队在国际权威期刊《Chaos, Solitons and Fractals》上发表了题为“Modeling two competing infectious diseases in a metropolitan contact network”的研究论文。我校为论文第一单位，应用统计本科生肖云竹与博士生李文杰为共同第一作者。

在都市化进程加速的背景下，高密度人口与复杂接触环境使得传染病传播风险显著增加。然而，现有研究多聚焦于单一疾病在均质网络中的传播，缺乏对都市特定环境下多病种竞争传播机制的系统探索。该研究创新性地构建了年龄分层的都市接触网络模型，揭示了两种竞争性传染病在校园、家庭、工作场所和社区四类典型环境中的传播规律，为精准防控策略的制定提供了理论依据。

研究团队基于全球大城市的人口普查数据，构建了覆盖0至85岁分层的接触网络，并采用维度缩减方法将高维动力学系统简化为一个方程。通过对纽约等大都市传播场景的数值模拟，验证了该方法的准确性，揭示系统存在三种关键传播模式（见图2）：当两种疾病的传播能力均较弱时，疫情难以暴发；当一种疾病明显优于另一种时，优势病种最终会完全抑制弱势病种；若两者传播能力相近且均较强，则可能实现长期共存。此外，研究还定量评估了不同环境对传播的影响，结果显示工作场所对高传播能力疾病的扩散具有显著促进作用

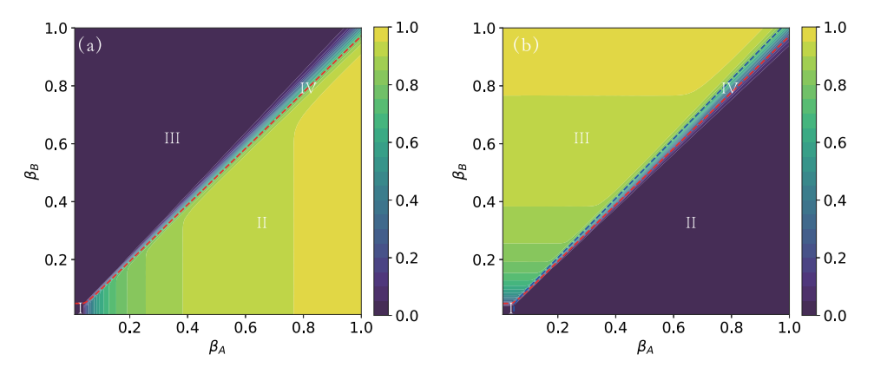
竞争性传染病传播终态的相图

研究成果不仅深化了对都市传染病传播动力学的理解，还可为跨学科研究提供方法论支持。例如，在公共卫生领域，模型可用于评估疫苗接种策略或非药物干预措施的效果；在城市规划中，可优化人群接触密集场所的布局设计以降低传播风险。研究团队表示，未来将进一步探索多病种协同传播机制及动态干预策略，推动研究成果向实际应用的转化。

期刊简介：

《Chaos, Solitons and Fractals》创刊于1991年，是国际非线性科学领域的重要期刊，专注于混沌理论、孤子动力学及分形结构等跨学科研究。该期刊为中科院一区（Top）、中信所一区。在非线性科学与复杂系统领域具有较高的学术影响力。该刊致力于发表理论创新与实证应用相结合的高质量研究，涵盖传染病动力学建模、城市复杂网络分析等前沿方向，旨在促进复杂系统理论的跨学科转化应用。

相关论文链接：

https://doi.org/10.1016/j.chaos.2025.116282